6.3 Volumes of Revolution
A solid of revolution is a solid obtained by rotating a region in the plane about an axis. The sphere, ellipsoid and right circular cone are familiar examples of such solids. Each of these is “swept out” as a plane region revolves around an axis (Figure 6.24).
We use the terms “revolve” and “rotate” interchangeably.
This method for computing the volume is referred to as the disk method because the vertical slices of the solid are circular disks.
Suppose that \(f(x) \ge 0\) for \(a \leq x \leq b\). The solid obtained by rotating the region under the graph about the \(x\)-axis has a special feature: All vertical cross sections are circles (Figure 6.25). In fact, the vertical cross section at location \(x\) is a circle of radius \(R = f(x)\) and thus \[ \textrm{Area of the vertical cross section} = \pi \ R^2 = \pi \ [f(x)]^2 \] We know from Section 6.2 that the total volume \(V\) is equal to the integral of cross-sectional area. Therefore, \(V = \int_a^b \pi \ [f(x)]^2\, dx\).
376
The cross sections of a solid of revolution are circles of radius \(R = f(x)\) and area \(\pi R^2 = \pi [f(x)]^2\). The volume, given by Eq. (1), is the integral of cross-sectional area.
Volume of Revolution: Disk Method
If \(f(x)\) is continuous and \(f(x)\ge 0\) on \([a,b]\), then the solid obtained by rotating the region under the graph about the \(x\)-axis has volume [with \(R=f(x)\)] \[ \begin{equation} \boxed{\bbox[#FAF8ED,5pt]{V = \pi \int_a^b R^2\, dx= \pi \int_a^b [f(x)]^2\, dx}} \tag {1} \end{equation} \]
EXAMPLE 1
Calculate the volume \(V\) of the solid obtained by rotating the region under \(y = x^2\) about the \(x\)-axis for \(0\le x \le 2\).
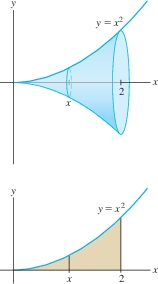
Solution The solid is shown in Figure 6.26. By Eq. (1) with \(f(x) = x^2\), its volume is \[ V = \pi\int_0^2 R^2\, dx = \pi\int_0^2 (x^2)^2\, dx = \pi\int_0^2 x^4\, dx = \pi\,\frac{x^5}{5}\bigg|_0^2 = \pi\frac{2^5}{5} = \frac{32}5\,\pi \]
Question 6.5 Volumes of Revolution Progress Check 1
Calculate the volume \(V\) of the solid obtained by rotating the region under \(y = x^5\) about the \(x\)-axis for \(0\leq x \leq 1\).
| A. |
| B. |
| C. |
| D. |
| E. |
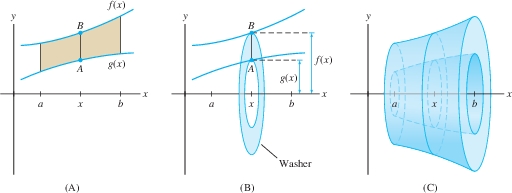
There are some useful variations on the formula for a volume of revolution. First, consider the region between two curves \(y = f(x)\) and \(y = g(x)\), where \(f(x) \ge g(x)\ge 0\) as in Figure 6.28(A). When this region is rotated about the \(x\)-axis, segment \(\overline{AB}\) sweeps out the washer shown in Figure 6.28(B). The inner and outer radii of this washer (also called an annulus; see Figure 6.27) are \[ R_{\textrm{outer}} = f(x),\qquad R_{\textrm{inner}} = g(x) \]
377
The washer has area \(\pi R_{\textrm{outer}}^2-\pi R_{\textrm{inner}}^2\) or \(\pi (f(x)^2 - g(x)^2)\), and the volume of the solid of revolution [Figure 6.28(C)] is the integral of this cross-sectional area: \[ \begin{equation} \boxed{\bbox[#FAF8ED,5pt]{V= \pi\int_a^b \big(R_{\textrm{outer}}^2 - R_{\textrm{inner}}^2 \big) \, dx = \pi\int_a^b \big(f(x)^2 - g(x)^2 \big) \, dx}}\tag {2} \end{equation} \] Keep in mind that the integrand is \((f(x)^2 - g(x)^2)\), not \((f(x) - g(x))^2\).

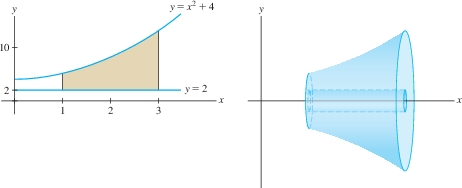
EXAMPLE 2 Region Between Two Curves
Find the volume \(V\) obtained by revolving the region between \(y=x^2+4\) and \(y = 2\) about the \(x\)-axis for \(1 \leq x \leq 3\).
Solution The graph of \(y=x^2+4\) lies above the graph of \(y = 2\) (Figure 6.29). Therefore, \(R_{\textrm{outer}}=x^2+4\) and \(R_{\textrm{inner}}=2\). By Eq. (2), \[ \begin{align*} V &=\pi\int_1^3 \big(R_{\textrm{outer}}^2-R_{\textrm{inner}}^2\big) \, dx = \pi\int_1^3 \big((x^2+4)^2-2^2\big) \,dx\\ &= \pi\int_1^3 \big(x^4+8x^2+12\big) \, dx =\pi \left(\frac15 x ^5+ \frac 83 x^3+12x \right)\bigg|_1^3 = \frac{2126}{15}\,\pi \end{align*} \]
Question 6.6 Volumes of Revolution Progress Check Question 2
Calculate the volume \(V\) of the solid obtained by rotating the region between \(y = \sqrt{x}\) and \(y = x\) about the \(x\)-axis for \(1\leq x \leq 4\).
| A. |
| B. |
| C. |
| D. |
| E. |
In the next example we calculate a volume of revolution about a horizontal axis parallel to the \(x\)-axis.
378
EXAMPLE 3 Revolving About a Horizontal Axis
Find the volume \(V\) of the “wedding band” [Figure 6.30(C)] obtained by rotating the region between the graphs of \(f(x)= x^2+ 2\) and \(g(x) = 4-x^2\) about the horizontal line \(y=-3\).

When you set up the integral for a volume of revolution, visualize the cross sections. These cross sections are washers (or disks) whose inner and outer radii depend on the axis of rotation.
Solution First, let's find the points of intersection of the two graphs by solving \[ f(x) = g(x)\quad\Rightarrow\quad x^2+2=4-x^2 \quad\Rightarrow\quad x^2=1\quad\Rightarrow\quad x=\pm 1 \] Figure 6.30(A) shows that \(g(x)\ge f(x)\) for \(-1\le x\le 1\).
If we wanted to revolve about the \(x\)-axis, we would use Eq. (2). Since we want to revolve around \(y=-3\), we must determine how the radii are affected. Figure 6.30(B) shows that when we rotate about \(y = -3\), \(\overline{AB}\) generates a washer whose outer and inner radii are both \(3\) units longer:
- \(R_{\textrm{outer}}=g(x)- (-3)=(4 -x^2) + 3 = 7-x^2\)
- \(R_{\textrm{inner}} =f(x)- (-3)= (x^2 +2) + 3 =x^2+5\)
We get \(R_{\textrm{outer}}\) by subtracting \(y= -3\) from \(y = g(x)\) because vertical distance is the difference of the \(y\)-coordinates. Similarly, we subtract \(-3\) from \(f(x)\) to get \(R_{\textrm{inner}}\).
The volume of revolution is equal to the integral of the area of this washer: \[ \begin{align*} \textrm{\(V\) (about \(y=-3\))}&= \pi\int_{-1}^1\big(R_{\textrm{outer}}^2 - R_{\textrm{inner}}^2\big)\, dx= \pi \int_{-1}^1 \Bigl((g(x)+3)^2- (f(x)+3)^2\Bigr)\,dx\\ & = \pi \int_{-1}^1\big((7-x^2)^2-(x^2+5)^2 \big)\,dx\\ &= \pi \int_{-1}^1\big((49-14x^2+x^4) - (x^4+10x^2+25)\big)\,dx\\ & = \pi\int_{-1}^1(24-24x^2)\,dx =\pi(24x-8x^3 )\Big|_{-1}^1 = 32\pi \end{align*} \]
EXAMPLE 4
Find the volume obtained by rotating the graphs of \(f(x) = 9 - x^2\) and \(y = 12\) for \(0 \leq x \leq 3\) about
- the line \(y=12\)
- the line \(y = 15\).
Solution To set up the integrals, let's visualize the cross section. Is it a disk or a washer?
In Figure 6.31, the length of \(\overline{AB}\) is \(12-f(x)\) rather than \(f(x)-12\) because the line \(y=12\) lies above the graph of \(f(x)\).
Figure 6.31(B) shows that \(\overline{AB}\) rotated about \(y=12\) generates a disk of radius \[ R = \textrm{length of \(\overline{AB}\)} = 12 - f(x) = 12 - (9-x^2)=3+x^2 \]
379
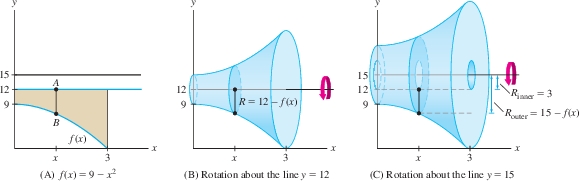 Figure 6.31: Segment \(\overline{AB}\) generates a disk when rotated about \(y=12\), but it generates a washer when rotated about \(y=15\).
Figure 6.31: Segment \(\overline{AB}\) generates a disk when rotated about \(y=12\), but it generates a washer when rotated about \(y=15\).The volume when we rotate about \(y=12\) is \[ \begin{align*} V = \pi\int_0^3 R^2\, dx &=\pi\int_0^3(3+x^2)^2\, dx=\pi\int_0^3(9+6x^2+x^4)\, dx \\ &=\pi \left(9x + 2 x^3 + \frac15x^5\right)\bigg|_0^3 = \frac{648}5\,\pi \end{align*} \]
- Figure 6.31(C) shows that \(\overline{AB}\) rotated about \(y=15\) generates a washer. The outer radius of this washer is the distance from \(B\) to the line \(y=15\): \[ R_{\textrm{outer}} = 15-f(x)=15-(9-x^2)=6+x^2 \] The inner radius is \(R_{\textrm{inner}}=3\), so the volume of revolution about \(y=15\) is \[ \begin{align*} V = \pi\int_0^3 \big(R_{\textrm{outer}}^2-R_{\textrm{inner}}^2\big)\,dx &= \pi\int_0^3 \big((6+x^2)^2 - 3^2\big)\, dx\\ & = \pi\int_0^3 (36 +12 x^2 + x^4 - 9)\, dx\\ &=\pi\left(27x +4x^3 + \frac15x^5\right)\bigg|_0^3 = \frac{1188}5\,\pi \end{align*} \]
Question 6.7 Volumes of Revolution Progress Check Question 3
The region bounded by the line \(y=1\) and the function \(y=\cos x\) where \(0 \leq x \leq 2\pi\) is rotated about the horizontal axis \(y=2\). Which integral represents the volume of the solid thus created?
| A. |
| B. |
| C. |
| D. |
We can use the disk and washer methods for solids of revolution about vertical axes, but it is necessary to describe the graph as a function of \(y\)—that is, \(x = g(y)\).
EXAMPLE 5 Revolving About a Vertical Axis
Find the volume of the solid obtained by rotating the region under the graph of \(f(x)=9-x^2\) for \(0 \leq x \leq 3\) about the vertical axis \(x=-2\).
Solution Figure 6.32 shows that \(\overline{AB}\) sweeps out a horizontal washer when rotated about the vertical line \(x=-2\). We are going to integrate with respect to \(y\), so we need the inner and outer radii of this washer as functions of \(y\). Solving for \(x\) in \(y=9-x^2\), we obtain \(x^2=9-y\), or \(x=\sqrt{9-y}\) (since \(x \geq 0\)). Therefore, \[ \begin{align*} R_{\textrm{outer}} &= \sqrt{9-y}+2,\qquad R_{\textrm{inner}}= 2\\ R_{\textrm{outer}}^2 - R_{\textrm{inner}}^2 &= \big(\sqrt{9-y}+2\big)^2 - 2^2 = (9-y)+4\sqrt{9-y}+4-4\\& = 9-y +4\sqrt{9-y} \end{align*} \] The region extends from \(y=0\) to \(y=9\) along the \(y\)-axis, so \[ \begin{align*} V = \pi\int_0^9 \big(R_{\textrm{outer}}^2-R_{\textrm{inner}}^2\big) \, dy &= \pi\int_0^9 \Big({9-y}+4\sqrt{9-y}\Big)\,dy\\ &= \pi \left(9y-\frac12y^2 -\frac83(9-y)^{3/2}\right)\bigg|_0^9=\frac{225}2\,\pi \end{align*} \]
380

Question 6.8 Volumes of Revolution Progress Check Question 4
Find the volume of the solid obtained by rotating the region enclosed by the graphs of \(y= 2 \sqrt {x}\) and \(y=x\) about the axis \(x=-2\)
| A. |
| B. |
| C. |
| D. |
| E. |
6.3.1 Summary
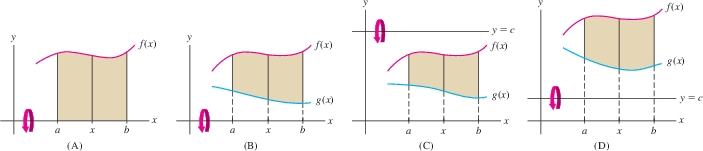
- Disk method When you rotate the region between two graphs about an axis, the segments perpendicular to the axis generate disks or washers. The volume \(V\) of the solid of revolution is the integral of the areas of these disks or washers.
- Sketch the graphs to visualize the disks or washers.
- Figure 6.33(A): Region between \(y=f(x)\) and the \(x\)-axis, rotated about the \(x\)-axis.
- Vertical cross section: a circle of radius \(R = f(x)\) and area \(\pi R^2 = \pi f(x)^2\): \[ V = \pi \int_a^b R^2\, dx = \pi \int_a^b f(x)^2\, dx \]
- Figure 6.33(B): Region between \(y=f(x)\) and \(y = g(x)\), rotated about the \(x\)-axis.
- Vertical cross section: a washer of outer radius \(R_{\textrm{outer}} = f(x)\) and inner radius \(R_{\textrm{inner}} = g(x)\): \[ V = \pi\int_a^b \big(R_{\textrm{outer}}^2 - R_{\textrm{inner}}^2\big) \, dx = \pi\int_a^b \big(f(x)^2 - g(x)^2 \big) \, dx \]
- To rotate about a horizontal line \(y=c\), modify the radii appropriately:
- Figure 6.33(C): \(c\geq f(x)\geq g(x)\): \[ R_{\textrm{outer}} = c - g(x),\quad\quad R_{\textrm{inner}} = c-f(x) \]
- Figure 6.33(D): \(f(x)\geq g(x)\geq c\): \[ R_{\textrm{outer}} = f(x) - c, \qquad R_{\textrm{inner}} = g(x) -c \]
- To rotate about a vertical line \(x=c\), express \(R_{\textrm{outer}}\) and \(R_{\textrm{inner}}\) as functions of \(y\) and integrate along the \(y\) axis.
381